MLP Neural Network in Regression

The MLP Neural Network is located under Machine Learning in Regression, on the left task pane. Alternatively, use the search bar for finding the MLP Neural Network algorithm. Use the drag-and-drop method or double-click to use the algorithm in the canvas. Click the algorithm to view and select different properties for analysis.

Properties of MLP Neural Network in Regression

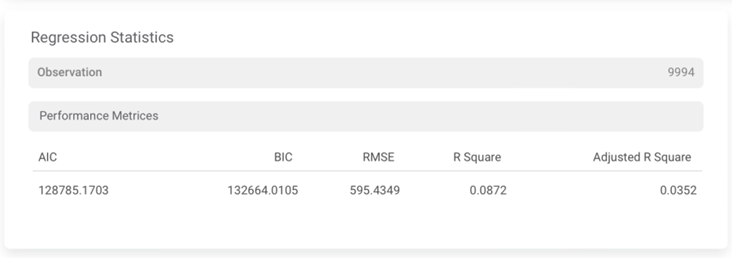
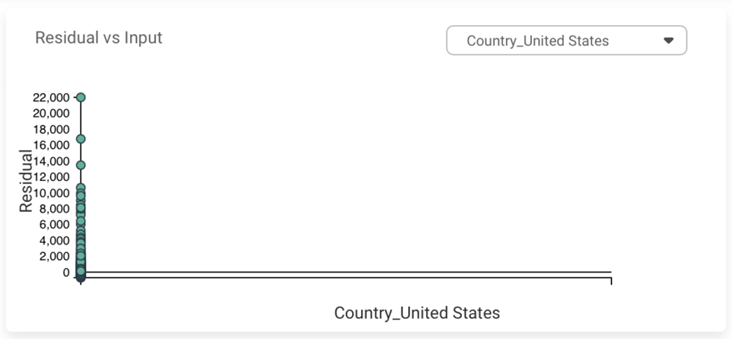
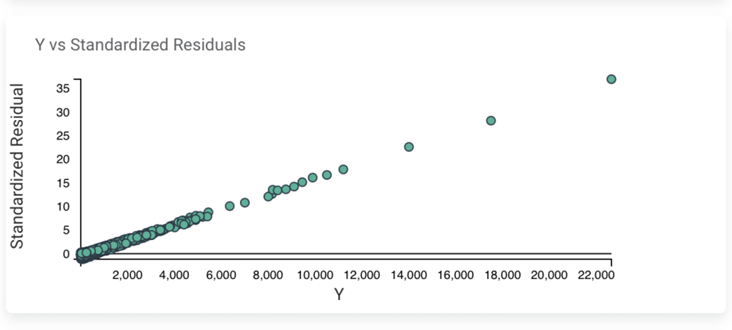
The available properties of MLP Neural Network are as shown in the figure given below:

Field		Description	Remark
Run		It allows you to run the node.	-
Explore		It allows you to explore the successfully executed node.	-
Vertical Ellipses		The available options are Run till node Run from node Publish as a model Publish code	-
Task Name		It displays the name of the selected task.	You can click the text field to modify the task name as required.
Dependant Variable		It allows you to select the dependent variable.	You can select only one variable, and it should be of Numeric type.
Independent Variable		It allows you to select the independent variable	You can choose more than one variable. You can select between Categorical and Numerical variables. Not any type only categorical and numerical. Because users consider all types try to run with text, geographical, and time series variables
Advanced	Learning_rate	It allows you to select the constant, in-scaling, or adaptive learning rate.	It is a hyperparameter that controls the step size at which the weights and biases of the network are updated during the training process.
	Learning_rate_init	It allows you to enter the learning rate value.	It refers to the initial learning rate used at the beginning of the training process.
	Hidden Layer Sizes	It allows you to enter the number of hidden layers. You can add multiple values separated by comma.	It refers to the number of neurons or units in each hidden layer of the network.
	Activation	It allows us to choose no-op, logistic sigmoid, hyperbolic tan, and rectified linear unit functions.	It is a mathematical function applied to the weighted sum of the inputs to each neuron in a hidden layer or the output layer.
	Solver	It allows us to choose lbfgs, sgd, and adam.	It refers to the optimization algorithm used to update the weights and biases of the network during the training process.
	Maximum Iterations	It allows us to enter the number of iterations. The default value is 200.	It refers to the maximum number of iterations or epochs that the training process will run.
	Random State	It allows us to enter the number of random states we want. The default value is 0.	It is a parameter that controls the random initialization of the network's weight and biases.
	Power_t	It allows us to select the power level. The default value is 0.5.	It determines the convergence criterion for the optimization algorithm.
	Dimensionality Reduction	It allows you to select between None and PCA.	It to the process of reducing the number of input features or variables in a dataset while preserving the important information and patterns present in the data.

Example of MLP Neural Network

In the example given below, the MLP Neural Network Regression is applied to the Superstore dataset. The independent variables are Country, City, and Category, etc. Quantity is selected as the dependent variable.

The result page displays the following sections.

Section 1 - Event of Interest

Performance Metric	Description	Remark
RMSE (Root Mean Squared Error)	It is the square root of the averaged squared difference between the actual values and the predicted values.	It is the most commonly used performance metric of the model.
R Square	It is the statistical measure that determines the proportion of variance in the dependent variable that is explained by the independent variables.	Value is always between 0 and 1.
Adjusted R Square	It is an improvement of R Square. It adjusts for the increasing predictors and only shows improvement if there is a real improvement.	Adjusted R Square is always lower than R Square.
AIC (Akaike Information Criterion)	AIC is an estimator of errors in predicted values and signifies the quality of the model for a given dataset.	A model with the least AIC is preferred.
BIC (Bayesian Information Criterion)	BIC is a criterion for model selection amongst a finite set of models.	A model with the least BIC is preferred.
MSE (Mean Squared Error)	It is the averaged squared difference between the actual values and the predicted values.	A model with low MSE is preferred.
MAE (Mean Absolute Error)	It the absolute value of difference between actual and predicted values	A model with low MAE is preferred.
MAPE ( Mean Absolute Percentage Error)	it is the average magnitude of error produced by a model, or how far off predictions are on average.	A model with low MAPE is preferred

Section 2 – Residuals Vs. Inputs

Section 3 – Y Vs. Standardized Residuals

Section 4 – Residuals Probability Plot